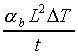The deflection calculated from the formula given above would then represent
the 1D deflection a beam would undergo. How do we calculate deflection
for a 2D surface like a PWB? And why does this affect the value used for
undeformed length?
First, apply the beam approximation to each edge of the PWB.

When the beams deform due a temperature change, the deflection can be
either up or down, depending on which side has the lower effective coefficient
of thermal expansion. (For temperature increases, deflection occurs toward
the side of lower thermal expansion.) Therefore, there are 4 possible deformed
configurations:




Notice that in all of these cases, if we assume that the deformation
at the edges completely defines the deformation within the interior of
the PWB, the total PWB deflection is the sum of the deflection at each
edge. Moreover, for both beams, the only variation is in the effective
undeformed length of the beam- the thickness, coefficient of bending, and
temperature change are constant. Therefore, these terms can be represented
by a constant term k, and we have:
by Pythagorean's theorem.
So, we use the diagonal undeformed length of the PWB because it allows
us to capture the 3D behavior of the deformed PWB.
To demonstrate that even with the geometric requirement that the shape
of the edges completely determines the shape of the interior and with quadratic
deformation curves it is still possibe to realistically model the 3D forms
of PWB warpage, we are providing a 3D surface viewer free here.

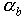 is
derivable from the material properties stored in the PWB Product model: the
relative coefficients of thermal expansion (CTE) of each major material,
the relative volumes of each material, and their respective elastic moduli.
However, we have adopted the simpler approach of establishing
is
derivable from the material properties stored in the PWB Product model: the
relative coefficients of thermal expansion (CTE) of each major material,
the relative volumes of each material, and their respective elastic moduli.
However, we have adopted the simpler approach of establishing 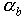 by
fitting it to experimental measurements of warpage. As of July 6, 1996,
we have only used data from [Yeh et. al., 1993], but we will shortly be
adding additional data points from [Stitler, 1996]. Note that since
by
fitting it to experimental measurements of warpage. As of July 6, 1996,
we have only used data from [Yeh et. al., 1993], but we will shortly be
adding additional data points from [Stitler, 1996]. Note that since 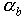 is
derived from the materials' CTEs, which vary according to temperature,
is
derived from the materials' CTEs, which vary according to temperature,
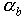 is
also a function of temperature.
is
also a function of temperature.

![]() =
=